马尔科夫不等式(Markov's Inequity)

定理(Markov's Inequity):

假设$X$是一个取值为非负数的随机变量，则对于任何的$t>0$，满足如下不等式:

$Pr[X\ge t] =\frac{E[X]}{t}$

证明:

令$Y$为一个布尔变量:

$$ Y=\begin{cases} 1 \quad X \ge t \\ 0 \quad X < t \end{cases} $$

则$Y$很明显满足:$E[Y]=Pr[Y=1]=Pr[X\ge t]$，所以:

$$ \begin{equation} Pr[X\ge t] = Pr[Y=1] = E[Y] \le E\bigg[\frac{X}{t}\bigg] = \frac{E[X]}{t} \end{equation} $$

$\Box$

马尔科夫不等式(Markov's Inequity)是一个非常有用的不等式工具，可以用来证明很多其他的不等式，包括后面将会说明的切比雪夫不等式(Chebyshev's Inequity).

应用举例

马尔科夫不等式一个典型应用是可以用来设计一个可以将Las Vegas算法转化为一个Monte Calo算法¹:

假设算法$A(x)$是一个针对某个判定问题的Las Vegas算法，且它运行时间的期望是$T(n)$,则我们可以设计一种方法将$A(x)$转化为具有单边错误的Monte Calo的算法$B(x)$:

$B(x)$:

运行$2T(n)$时长的$A(x)$算法。
如果$A(x)$返回一个结果，则将该结果直接返回;如果$A(x)$没能返回结果，就直接返回1.

可以看到，$B(x)$是一个运行时间确定，但是返回结果不确定的算法，也即是Monte Calo算法。并且，只有当$A(x)$没有返回结果时，才有可能返回错误解。这是False Postive的单边错误类型。我们可以来计算一下$B(x)$返回一个错误的解的概率，在这计算过程中，我们就需要用到马尔科夫不等式了。

$$ \begin{equation} Pr[返回错误解]\le Pr[A(x)的运行时间\ge 2T(n)] \le \frac{E[A(x)的运行时间]}{2T(n)} = \frac{T(n)}{2T(n)} = \frac{1}{2} \end{equation} $$

方差(Variance)

定义: 一个随机变量$X$的方差定义为:

$Var[X] = E[(X-E[X])^2] = E[X^2] - E[X]^2$

一个随机变量$X$的标准差定义为:

$\delta[X]=\sqrt{Var[X]}$

需要注意的是，方差和期望不一样，是不满足线性可加性的。

定义: 两个随机变量的协方差定义为:

$Cov(X,Y)=E[(X-E[X])(Y-E[Y])]$

定理: 对于任意的随机变量$X_1,X_2,\cdots,X_n$,有:

$Var\bigg[\sum\limits_{i=1}^n X_i \bigg] = \sum\limits_{i=1}^n Var[X_i] + \sum\limits_{i\neq j}Cov(X_i,X_j)$

证明: 这只需要证明两个随机变量的情况。假设有两个随机变量$X$,$Y$，则

$$ \begin{aligned} Var[X+Y] &= E\big[(X+Y-E[X+Y])^2\big] \\ &= E\big[(X-E[X]+Y-E[Y])^2\big] \\ &= Var[X] + Var[Y] +2Cov(X,Y) \end{aligned} $$

$\Box$

定理: 对于任何两个独立的随机变量$X$和$Y$,有:

$E[X\cdot Y]=E[X]\cdot E[Y]$

证明: 假设$X,Y$是两个相互独立的随机变量，则我们可以做如下的推导:

$$ \begin{aligned} E[X\cdot Y] &= \sum\limits_{xy}Pr[X=x\wedge Y=y] \\ &= \sum\limits_{xy}xPr[X=x]yPr[Y=y]\\ &= \sum\limits_{x}xPr[X=x]\sum\limits_{y}yPr[Y=y]\\ &=E[X]\cdot E[Y] \end{aligned} $$

$\Box$

上述第二个等号之所以成立，是因为$X,Y$相互独立。

利用上述的定理，我们可以证明下面的定理:

对于任何两个独立的随机变量$X,Y$，它们的协方差为0:

Cov(X,Y) = 0

证明:

$$ \begin{aligned} Cov(X,Y) &= E\big[(X-E[X])(Y-E[Y])\big] \\ &= E\big[X-E[X]\big]E\big[Y-E[Y]\big]\\ &= 0 \end{aligned} $$

$\Box$

利用上述的结论，我们可以直接得到下面结论:

定理: 对于两两独立的随机变量$X_1,X_2,\cdots,X_n$来说，有:

$$Var\bigg[\sum\limits_{i=1}^n X_i \bigg] = \sum\limits_{i=1}^n Var[X_i]$$

伯努利分布的方差

对于满足伯努利分布的$X$来说，有:

$$ \begin{equation} X = \begin{cases} 1 \quad p \\ 0 \quad 1-p \\ \end{cases} \end{equation} $$

则其方差可以直接计算:

$$ \begin{equation} Var[X] = E[X^2] - E[X]^2 = p - p^2=p(1-p) \end{equation} $$

二项式分布的方差

二项分布是n个独立的伯努利实验，因此，如果$Y$是满足二项分布的话，则$Y=\sum\limits\_{i=1}^n X\_i$，利用独立性条件，$Y$的方差可以直接计算:

$$ \begin{equation} Var[Y] = Var\bigg[\sum\limits_{i=1}^n X_i\bigg] = \sum\limits_{i=1}^n Var[X_i] = \sum\limits_{i=1}^n p(1-p) = np(1-p) \end{equation} $$

切比雪夫不等式(Chebyshev's Inequity)

在概率统计中，切比雪夫不等式(Chebyshev's Inequity)是一个非常重要的不等式，它给出了比Markov不等式更强的界。它表述如下:

对于任何的$t>0$，都满足:

$$Pr[\vert X-E[X] \vert \ge t] \le \frac{Var[X]}{t^2}$$

证明:

首先，如下等式是肯定成立的:

$$ \begin{equation} Pr[\vert X-E[X] \vert \ge t] = Pr[( X-E[X] )^2 \ge t^2] \end{equation} $$

我们可以将$(X-E[X])^2$整体看成是一个随机变量，且这个随机变量是非负的，因此我们直接套用Markov不等式:

$$ \begin{aligned} Pr[\vert X-E[X] \vert \ge t] &= Pr[( X-E[X] )^2 \ge t^2] \\ &\le \frac{E\bigg[(X-E[X])^2 \bigg]}{t^2} \\ &= \frac{Var[X]}{t^2} \end{aligned} $$

$\Box$

问题举例

中位数选择(Median Selection)

中位数选择问题也是一个比较常见的问题，从一个集合$S$中选择第$\lceil\frac{n}{2}\rceil$小的数.其实这个问题可以进行推广到从集合中选取第$k$小的数²,但是在这里我们暂时只讨论特殊情况:只寻找集合$S$中的中位数。这个寻找过程很直接地可以利用排序来完成，一旦将$S$排好序了，自然就能找到任意$k$小的元素了。但是，排序算法的最好代价是$O(n\log n)$，而如果我们利用随机算法的方法的话，可以将时间代价降低为线性时间³。

这个随机化的算法被称为是LazySelect，其基本思想是:如果我们能够从集合$S$中寻找到满足如下条件的元素$d$和$u$:

中位数$m$存在于$[d,u]$中，也即$m$满足$d\le m\le u$
位于$d$和$u$之间的元素足够少，也即$C=\\{x\in S \big\vert d\le x\le u\\},\vert C \vert = o(\frac{n}{\log n})$，使得$C$能在线性时间内排序。

如果我们能找到这样的$d,u$的话，那么我们就能够在线性时间内找到中位数$m$.

假设我们已经找到了这样的$d,u$,那么我们只需要计算如下的步骤:

从$S$中计算出小于$d$的元素个数$l\_d$
将$C$排序，由于$\vert C\vert = o(\frac{n}{\log n})$,因此$C$的排序能够在线性时间内完成。
在排好序的$C$中，第$\lfloor \frac{n}{2} \rfloor-l_d+1$个元素就是我们需要求的$m$

好了，那么我们如何才能快速地找到满足条件的$d,u$呢？事实上，$d,u$需要满足的条件并不是非常严格的，是一种比较"粗粒度"的约束条件，那我们就可以利用随机取样的方法来得到$d,u$，具体做法是这样的:

从$S$中随机取样得到一个子集$R$
将$R$排序，在$R$的中位数附近寻找这样的$d,u$
如果寻找的$d,u$满足上述的条件，那我们就能在线性时间内找到$S$的中位数，否则算法失败。

在这个过程中，有两个参数很重要，一是子集$R$的大小，既不能太小，从而导致不能找到合适的$d,u$;也不能太大，从而导致不能在线性时间内排序。二是$d,u$的选择范围，如果$d,u$靠得很近，很有可能$m$就不在$C$中了，如果$d,u$分得很开，那么会导致$\vert C\vert$很大，不能在线性时间内完成排序。

在这个算法中，我们选取$R$的大小为$n^{\frac{3}{4}}$,而$d,u$是$R$的中位数的$\sqrt{n}$的范围⁴。整体的算法步骤如下所示:

input: 一个有$n$个元素的集合$S$

output: $S$的中位数$m$

从$S$中随机取样得到一个大小为$\lceil n^{\frac{3}{4}}\rceil$的子集$R$
将$R$进行排序
令$d$为排好序的集合$R$中的第$\lfloor \frac{1}{2}n^{\frac{3}{4}} - \sqrt{n} \rfloor$小的元素
令$u$为排好序的集合$R$中的第$\lceil \frac{1}{2}n^{\frac{3}{4}} + \sqrt{n} \rceil$小的元素
遍历$S$中的元素，计算出集合$C=\{x\in S: d\le x\le u \}$，以及$l_d=\vert\{ x\in S: x < d \} \vert$,$l_u=\vert x\in S: x > u \vert$
如果$l_d >\frac{n}{2}$或者$l_u > \frac{n}{2}$，则算法失败。
如果$\vert C \vert \le 4n^{\frac{3}{4}}$,则将$C$排序;否则算法失败。
在排好序的$C$中，返回$\lfloor \frac{n}{2} \rfloor-l_d+1$小的元素。

在上述的算法步骤中，第6步是用来保证$d,u$存在于$C$之中，而第7步是用来保证$\vert C\vert$足够小，能够在线性时间内完成排序。

现在我们需要来分析一下这个算法，首先我们需要定义三个事件:

$\epsilon_1$: $Y_1 = \vert \{ r\in R \vert r \le m \} \vert < \frac{1}{2}n^{\frac{3}{4}} - \sqrt{n}$
$\epsilon_2$: $Y_2 = \vert \{ r\in R \vert r \ge m \} \vert < \frac{1}{2}n^{\frac{3}{4}} - \sqrt{n}$
$\epsilon_3$: $\vert C \vert > 4n^{\frac{3}{4}}$

很显然，事件$\epsilon_1,\epsilon_2$对应于步骤6中的两个判断条件，因为如果$l_d>\frac{n}{2}$,则$R$中的所有元素都在中位数$m$的右侧，即$R$中第$\frac{1}{2}n^{\frac{3}{4}} - \sqrt{n}$小的元素一定大于$m$.同理$l_u > \frac{n}{2}$等价于事件$\epsilon_2$.而$\epsilon_3$等价于上述算法中的步骤7.

从整个算法的步骤中，我们可以看到，当前仅当$\epsilon_1,\epsilon_2,\epsilon_3$中的其中之一发生时，算法才会失败，否则一定会返回出一个正确的解。

现在我们就需要来计算一下$\epsilon_1,\epsilon_2,\epsilon_3$中至少有一个发生的概率是多少。

$\epsilon_1$和$\epsilon_2$是类似的，因此我们首先来看一下$\epsilon_1$发生的概率是多少。

定义$X_i$为一个布尔值:

$$ \begin{equation} X_i = \begin{cases} 1 \quad 如果的i个样本小于等于中位数m \\ 0 \quad 如果的i个样本大于中位数m \end{cases} \end{equation} $$

则$Y_1=\sum\limits_{i=1}^{n^{\frac{3}{4}}}X_i$,而$Pr[X_i=1]$可以进行如下的计算:

$$ \begin{equation} p = Pr[X_i=1] = \frac{1}{n}\lceil \frac{n}{2} \rceil \ge \frac{1}{2} \end{equation} $$

而此时的$Y_1$是一个二项分布，因此

$$ \begin{aligned} E[Y_1] &= n^{\frac{3}{4}}p \ge \frac{1}{2}n^{\frac{3}{4}} \\ Var[Y_1] &= n^{\frac{3}{4}}p(1-p) \le \frac{1}{4}n^{\frac{3}{4}} \end{aligned} $$

因此，我们可以应用Chebyshev不等式:

$$ \begin{aligned} Pr[\epsilon_1] &= Pr\bigg[Y_1<\frac{1}{2}n^{\frac{3}{4}} - \sqrt{n}\bigg] \\ &= Pr\bigg[Y_1-\frac{1}{2}n^{\frac{3}{4}}<-\sqrt{n}\bigg] \\ &\le Pr\bigg[\vert Y_1 - E[Y_1]\vert < \sqrt{n}\bigg] \\ &\le \frac{Var[Y_1]}{n} \\ &= \frac{1}{4}n^{-\frac{1}{4}} \end{aligned} $$

因此，$\epsilon_1$发生的概率不大于$\frac{1}{4}n^{-\frac{1}{4}}$.同理，$\epsilon_2$发生的概率也同样不会超过$\frac{1}{4}n^{-\frac{1}{4}}$.

现在我们来分析一下$\epsilon_3$的情况。

如果$\epsilon_3$发生的话，那么根据鸽巢原理，如下两个事件至少会发生一个:

$\xi_1$: 在$C$中至少有$2n^{\frac{3}{4}}$个元素大于$m$
$\xi_2$: 在$C$中至少有$2n^{\frac{3}{4}}$个元素小于$m$

我们只需要分析一种情况，另外一种情况利用对称性就能得到了。

我们来分析$\xi_1$，如果$\xi_1$成立，那么$u$在排好序的$S$中的位置至少为$\frac{1}{2}n+2n^{\frac{3}{4}}$到这里位置应该还是比较好理解的，但是接下来的结论会有点绕，所以我先用一个图来说明一下目前$S$的划分情况:

mid

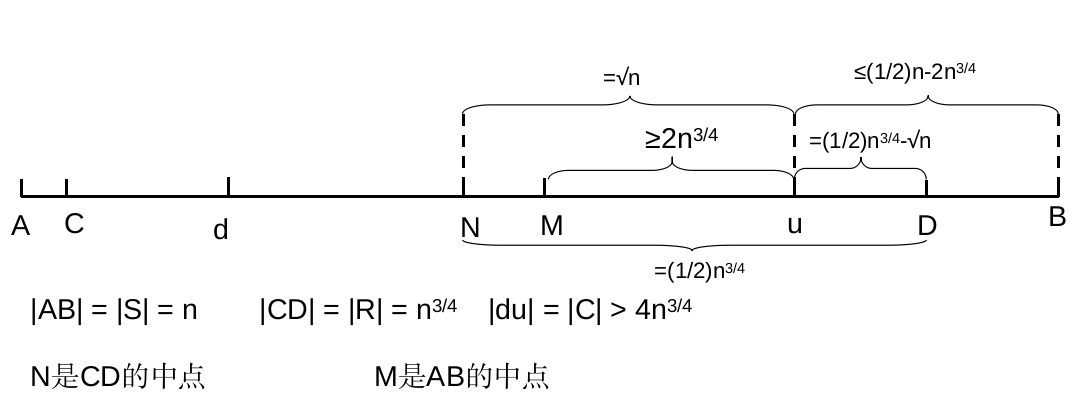
从图中可以看到，如果$\xi_1$成立的话，我们就能得到如下的结论:集合$R$中至少有$\frac{1}{2}n^{\frac{3}{4}}-\sqrt{n}$个元素是在$S$的前$\frac{1}{2}n-2n^{\frac{3}{4}}$大的元素集合中.从图上来看，就是$uD$一定是属于$uB$的，而$\frac{1}{2}n^{\frac{3}{4}}-\sqrt{n}$和$\frac{1}{2}n-2n^{\frac{3}{4}}$分别是$uD$和$uB$的长度。⁵

在得出上述的结论之后，后面的计算就比较简单了:

定义$X_i$为一个布尔值:

$$ \begin{equation} X_i = \begin{cases} 1 \quad 第i个样本处于uB\\ 0 \quad 第i个样本不处于uB \end{cases} \end{equation} $$

同时令$X=\sum\limits_{i=1}^{n^{\frac{3}{4}}}X_i$为所有落入$uD$之间的元素的总数。

又因为

$$ \begin{equation} p=Pr[X_i=1] = \frac{\frac{1}{2}n-2n^{\frac{3}{4}}}{n} = \frac{1}{2} - 2n^{-\frac{1}{4}} \end{equation} $$

且$X$是一个二项分布，因此:

$$ \begin{equation} E[X] = n^{\frac{3}{4}}p=\frac{1}{2}n^{\frac{3}{4}} - 2\sqrt{n} \\ Var[X] = n^{\frac{3}{4}}p(1-p) = \frac{1}{4}n^{\frac{3}{4}} - 4n^{\frac{1}{4}} < \frac{1}{4}n^{\frac{3}{4}} \end{equation} $$

最后应用Chebyshev不等式,我们得到:

$$ \begin{aligned} Pr[\xi_1] &= Pr\bigg[X\ge \frac{1}{2}n^{\frac{3}{4}}-\sqrt{n}\bigg]\\ &\le Pr\bigg[ \vert X-E[X] \vert \ge \sqrt{n} \bigg]\\ &\le \frac{Var[X]}{n} \\ &\le \frac{1}{4}n^{-\frac{1}{4}} \end{aligned} $$

因此，$Pr[\epsilon_3]\le Pr[\xi_1] + Pr[\xi_2]\le \frac{1}{2}n^{-\frac{1}{4}}$

综合上面对$\epsilon_1,\epsilon_2,\epsilon_3$的分析，我们最终得到如下的界:

$$ \begin{equation} Pr[\epsilon_1] + Pr[\epsilon_2] + Pr[\epsilon_3] \le n^{-\frac{1}{4}} \end{equation} $$

因此，说明算法失败的概率是比较小，能够以较大的概率在线性时间内找到正确的中位数。

参考资料

wiki:Moment
wiki: Markov's Inequity
wiki: Chebyshev's Inequity
wiki:Monte Calo algorithm
wiki:Las Vegas algorithm
Probability and Computing:Randomized Algorithms and Probabilistic Analysis

Las Vegas算法是指运行时间不确定，但是运行结果一定正确的一类随机算法。而Monte Carlo算法是指运行时间确定，但是运行结果不一定正确的一类随机算法。这两个算法的概念我在随机算法学习笔记0-概率空间&计算模型中详细说明了。 ↩
这里的集合$S$是乱序的。 ↩
其实也存在能够在线性时间内解决中位数的确定性算法的，但是这个算法比较复杂，以前曾经实现过一次，但是现在已经基本不记得了。感兴趣的朋友可以查看这里 ↩
这些数值是如何得出的，其实我也说不清，这些数值完全是凑出来的，是为了方便后续的计算而硬凑出来的。 ↩
这个结论至关重要，是后面一系列计算的基础，但是我看过的资料上这部分结论都是直接得出的，没有相似的说明，这张图也是我自己研究了半天之后才画出的，应该对理解如何得出这个结论会有帮助,这部分确实需要好好想想才能想通。 ↩

Flyaway is the owner of this blog.

随机算法学习笔记3-矩(Moment)和方差(Deviation)

马尔科夫不等式(Markov's Inequity)

应用举例

方差(Variance)

伯努利分布的方差

二项式分布的方差

切比雪夫不等式(Chebyshev's Inequity)

问题举例

中位数选择(Median Selection)

参考资料

Reading Time

Published

Category

Tags

Contact