多元多项式判定问题(PIT)

在之前的学习笔记0 中，曾经分析过这个问题，但是，当时是对于单元多项式进行分析的，这要比多元的情况要简单得多。这次，我们将来看一下多元多项式的判定问题。

多元多项式判定问题可以表述成:

---

input: 定义在数域F上度为d的多元多项P1(x1,x2,⋯,xn),P2(x1,x2,⋯,xn)

output: 如果P1(x1,x2,⋯,xn)≡P2(x1,x2,⋯,xn)，则返回Yes，否则返回No

---

注意，在这里多元多项式的度是指每一项中所有变元的指数之和的最大值。

利用随机算法可以很巧妙地设计一种算法思路，首先令Q(x1,x2,⋯,xn)=P1(x1,x2,⋯,xn)−P(x1,x2,⋯,xn)，则原问题可以转化为判断D(x1,x2,⋯,xn)≡0是否成立。

一个和学习笔记0中相似的算法可以用来进行判断:

---

Algorithms for PIT

1. 从F中随机取出一个若干个数，形成集合S
2. 从S中随机取出r1,r2,⋯,rn,形成向量→r
3. 如果D(r1,r2,⋯,rn)=0,则返回Yes，否则返回No

---

现在我们要来分析这个算法的正确性。

我们的分析过程可以用归纳法:

首先，当n=1时，则多元多项式退化为单元多项式，根据在学习笔记0中的分析，使用该算法的情况下，单元多项式判断出错的概率是

我们假设在n=k−1时，Pr[D(r1,r2,⋯,rk−1)]≤d|S|成立。

则当n=k时，可以D(x1,x2,⋯,xn)表示成:

其中，t表示x1的最大指数，这也就意味着，对于Dt来说，它的度最大是d−t,同时Dt≢0

特别的，我们可以将D写成如下的特殊形式:

注意，这里的ˉD(x1,x2,⋯,xk)中是不含xt1这一项的。

根据归纳法的证明步骤，在我们现在需要证明Pr[D(r1,r2,⋯,rk)=0]≤d|S|

首先，令ϵ表示事件"Dt(r2,r3,⋯,rk)=0"我们可以利用全概率法则，将D(r1,r2,⋯,rk)展开成:

对于Dt(x2,x3,…,xk)来说，它满足以下三点性质:

1. Dt来说，它有k−1个未知数，也即k−1个变元
2. Dt的度最大不会超过d−t
3. Dt≢0

则根据我们之前的假设，应该有

而当Dt(r2,r3,⋯,rk)≠0也即⌝ϵ成立时，令

则，G有如下三点性质:

1. G(x1)是一个单元多项式
2. G(x1)≢0
3. G(x1)的度为t(因为Dt(r2,r3,⋯,rk)≠0,所以xt1一定存在,同时ˉD(x1,r2,⋯,rk)中又不包含x_1t这一项)

所以有

而根据???的等式，我们可以做如下变换:

而上式中右侧的Pr[ϵ]和Pr[D(→r=0)|¬ϵ]可以通过???和???进行计算，因此我们就能得到:

◻

综上，我们证明了当P_1,P_2为多元多项式时，该算法依然能保持d|S|的概率返回错误解，利用独立重复运行的方法，可以将这个错误率进一步减小，因此这就证明了该算法的可行性。

最小割问题

现在我们来看另外一个问题——最小割问题，最小割问题的描述比较复杂,具体问题描述可以从wiki上找到，这里我就不多阐述了，直接来看一下解决这个问题的随机化的算法吧。

首先，我们需要定义一种"合并(contract)"操作，它将图中一条边上的两个定点合并，但是除了这两个点之间的边以外的边均保持不变(有可能因此会形成平行边)。

如下图所示，粗边被contract之后就得到右边的图了。

{% asset_img min-cut.png 最小割 %}

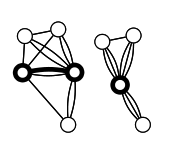
在定义了contract操作之后，我们就能够在图G(V,E)上构造我们随机化的算法了:

---

RandomContract(Karger 1993)

while |V|>2 do: {

• 随机地从G中选出一条边e
• 对于e执行contract操作,G = contract(G,e)

} return E

---

算法最终返回的是只有两个点的图，而这两点中有着很多的平行边，而此时所有平行边的个数就是我们最小割中边的个数。

还是一样的，我们需要分析这个算法的正确性。

首先，我们需要引入两个引理:

引理1: 如果选取的e不存在于最小割C中，则contract(G,e)中的最小割大小不会超过G中的最小割大小。也即，contract操作不会破坏最小割。

证明: 因为最小割C将图分成两部分，假设分别是P和Q，则现在只有三种边，分别属于C,P和Q，而我们的前提条件是e∉C，所以e之能是属于P或Q，因此并不会改变原来的C.◻

引理2: 如果C是G(V,E)中的最小割，则|E|≥|V||C|2

证明: 因为C是G(V,E)中的一个最小割，则说明G中所有的点的度都至少为C，则边集的大小至少为|V||C|2，也即|E|≥|V||C|2 ◻

有了这两个引理，我们可以开始对Karger算法进行分析了。

很显然，要该算法返回正确的结果，就必须保证每次随机选择的边e均不能属于C，因为一旦C中的边contract了，则最小割就被破坏了，算法会返回出一个错误的结果。

考虑单次随机选择的情况，假设前面的i−1次随机选择都没有选取到C中的边，则第i次依然没有选取C中的边的概率为:

其中E_i表示经过i−1次选取之后，图中剩余的边集。

而根据引理2，我们可以得到:

其中Vi表示经过i−1次选取之后，图中剩余的点集。而又因为，每一次的contract操作都会减少一个点，因此Vi=n−i+1

令ϵ表示事件"在n−2次选择中，都没有选中C中的边"

因此在整个算法过程中，C中没有边被选中的概率为:

这就说明，每一次运行该算法，能够以n(n−1)2的概率得到正确的结果，因此，如果我们独立重复执行该算法n(n−1)次，然后最终返回一个最小的C，则返回一个正确解的概率是:

这个结果很好，因为它是一个和n无关的常量！

Share on: Twitter ❄ Facebook ❄ Email

---

---