Chernoff Bound

切尔诺夫界(Chernoff Bound)通常是用来描述随机变量的和的取值在其期望附近的概率，在大多数情况下，随机变量都具有"集中"现象，也即概率较高的取值都集中在其期望附近。比如说抛硬币,抛一次硬币也许无法确定出现正面的概率，但是抛10000次之后呢？出现正反面的概率都稳定在了12附近，这就是"概率集中"现象，而切尔诺夫界(Chernoff Bound)就可以定量的来描述这种现象。

切尔诺夫界(Chernoff Bound)的证明主要用到了两个工具，一是Markov不等式,一是Moment Generating Functions.之前的几篇笔记中已经证明过Markov不等式了，所以这里先介绍一下Moment Generating Function.

Moment Generating Functions

定义: Moment Generating Functions

随机变量X的Moment Generating Functions定义为:

MX(t)=E[etX]

从定义中可以看到，

是关于t的函数，而不是X。利用如下的泰勒展开式:

我们可以得到:

因此，Moment Generating Functions这个函数实际上是包含了X的所有阶的信息.

证明Chernoff Bound

定理(Chernoff Bound)

假设X=n∑i=1Xi,且X1,X2,⋯,Xn是独立的泊松实验¹，其中μ=E[X]. 则对于任何的δ>0,有:

Pr[X≥(1+δ)μ]≤(eδ(1+δ)1+δ)μ

证明:

首先根据指数函数的递增性，我们有:

由此将原来的不等式和Moment Generating Functions联系了起来。利用Markov Inequity得到:

然后我们计算E[etX]:

上述化简过程中的最后一个等号是因为Xi是相互独立的。

令pi=Pr[Xi=1],则:

因为E[etXi]可以计算为:

上式中的最后一个不等号是因为根据泰勒展开式,当y>0时，有ey≥1+y.

因此:

将其代回原来的Markov Inequity:

令t=ln(1+δ),我们就得到:

◻

小结

Chernoff Bound一共有三个条件:

1. X必须是多个随机变量的和
2. 每一个Xi必须是独立的
3. Xi是一个0-1取值的随机变量(这不是必须的，但是0-1变量比较容易计算)

从上述证明步骤来看，证明的主要流程有以下几点:

1. 利用了Moment Generating Functions和Markov Inequity
2. 计算E[etXi]，其中需要用到泰勒展开式
3. 选取合适的t

另外还有一些Chernoff Bound的变形形式:

Chernoff Bound其他形式

假设X=n∑i=1Xi,且X1,X2,⋯,Xn是独立的泊松实验，其中μ=E[X]. 则

1.对于0<δ≤1有:

$Pr[X\ge (1+\delta)\mu]< exp\bigg(-\frac{\mu\delta^2}{2} \bigg) $

$Pr[X\le (1-\delta)\mu]< exp\bigg(-\frac{\mu\delta^2}{2} \bigg) $

2.对于t≥2eμ，有:

Pr[X≥t]≤2−t

Packet Routing

这个Packet Routing问题是来自于并行计算领域，描述的是，假如我们有N个处理器，这些处理器之间需要进行信息交互，那这些处理器就构成了一个网络，处理器在这个网络中通过发包和收包来进行信息的交互。构成的图有如下的限制:

1. 每一个处理器有且仅有一个独一无二的目的地
2. 信息传递是同步的，每一条边每次最多只能传递一个数据包。

可以试想一下，如果构成的图结构是一个完全图²，那么每次只需要一轮传递，就能把所有的包送达到目的地。但是，在很多的实际情况中，完全图是无法实现的，考虑到成本问题，图结构应该是比较稀疏的(具有很少的边)，因此两个节点进行信息交互的时候，需要经过多条边的传递才能完成一次交互。在这种情况下，当有大量的数据包需要传递的时候，必然会导致网络的堵塞和瓶颈，我们的目的就是要能够设计出一种尽量稀疏的网络结构及其相应的路由算法，使得任意两点间进行信息交互的时候经过尽量少的边。

Hypercube

现在我们来考虑一个比较特殊的图结构——Hypercube.所谓的Hypercube，是一种特殊的无向图，它有N个节点，且N=2d，其中d是一个正整数，称为Hypercube的度。Hypercube中的每一个点都用一个二进制串{0,1}d来表示。节点u,v有边当且仅当u,v之间仅有一位是不同的，也即是u和v的Hamming Distance为1。

下图是度为1-4时，Hypercube的例子:

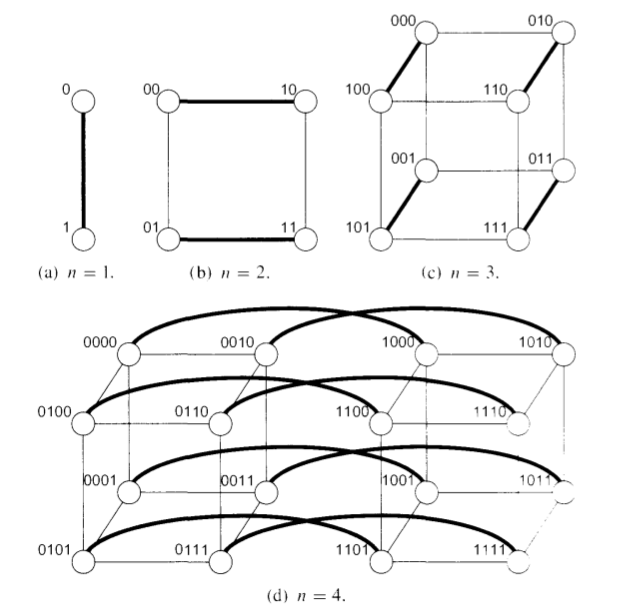
根据Hypercube的定义，我们可以知道这样一个性质:对于图中任何一个点对(u,v),它们之间的距离³最多为d.这是因为从一个点到另外一个点最多会有d位完全不一致。

这个性质给了我们不小的启发，我们可以轻易地设计如下的路由算法:

---

Bit-Fixing Routing Algorithm

For each packet:

1. Let u,v∈{0,1}d be the origin and destination of the packet respectively.

2. For i = 1 to d,do:

   if ui≠vi then traverse the edge (v1,⋯,vi−1,ui,⋯,ud)→(v1,⋯,vi−1,vi,ui+1,⋯,ud)

---

在实际情况下，在并行的路由N个数据包的时候，很有可能会出现同一条边同时被多个数据包使用，而根据之前的定义，每一条边一次最多只能通过一个数据包，因此我们需要为每一条边设计一个排队策略，可以是FIFO(First In First Out)或者FTG(Furthest To Go).

但是，对于上述的Bit-First Routing Algorithm算法来说，无论设计的是什么样的排队策略，总会有存在一个目的地的排列,使得需要通过Ω(√N)轮才能将所有的N个数据包路由到起各自的目的地。这是最坏的情况，但是在这里我们将会只分析这个算法的平均情况，分析的过程中就将会使用到之前的证明的Chernoff Bound.

平均情况分析

首先，我们将原问题进行一下放松，不再约束每一个处理器必须有独一无二的目的地，而可以是图上的任意一点。对于平均情况来说，任意一个起始点v的目标点是{0,1}d的一个均匀且独立的分布,我们用Pv表示点v到其随机目的地r的路径，Pv是一个边的序列。

显然，如果Pv和Pu有公共的边，那么u,v就有可能会发生堵塞现象,我们需要对此进行分析。

令Huv为一个指示变量，用来说明Pu和Pv是否有公共边:

根据上述的定义，显然我们可以得到

，Hu表示所有经过Pu的路径的数目，这是u被延迟的次数的一个上界。

由于u,v的目的地点都是独立选取的，因此Huv之间也是相互独立的，因此我们可以使用Chernoff Bound.

令e表示图中的边，T(e)表示经过边e的路径的数目,则我们可以得到:

因此：

令|Pv|表示路径Pv的长度，这里的长度其实就是起始点与目标点之间的不同的位数，又因为目的地点是均匀分布的，所以E[|Pv|]=d2，因此我们得到:

又因为"所有的点的路径长度之和"和"每一条边上经过的路径的数目之和"是相等的，因此可以得到:

则:

又因为T(e)是同分布的，因此每一个E[T(e)]是相等的，而对于一个Hypercube来说，一共有dN2条边，因此:

而Pu的长度最多为d，因此根据???，我们可以得到:

应用Chernoff Bound

我们可以是用Chernoff Bound的第二种变形形式:

当t≥2eμ时，Pr[X≥t]≤2−t

取t=6d>2eE[Hu]=2ed,应用Chernoff Bound:

此时我们只是给定了指定的Hu的一个上界，对于整个图的来说，我们需要应用Union Bound:

参考资料

• wiki:Chernoff Bound
• wiki:Markov Inequity
• wiki:Moment Generating Function
• wiki:Hypercube
• wiki:HammingDistacne

Share on: Twitter ❄ Facebook ❄ Email

---

---