向量范数

定义

定义: 如果$V$是数域$F$上的线性空间，且对于$V$中任意一向量$x$，对应着一个实值函数$\Vert x \Vert$，它满足下面三个条件:

$\Vert x \Vert\geq 0;\Vert x \Vert = 0 \Leftrightarrow x=0$ 正定性
$\Vert\alpha x \Vert = \vert\alpha\vert \cdot \Vert x \Vert$，对$\forall\alpha\in F$ 齐次性
$\Vert x+y \Vert\leq \Vert x\Vert + \Vert y \Vert$ 三角不等式

则称$\Vert x \Vert$为$V$上向量$x$的范数(norm)¹

定义: 定义了向量范数$\Vert . \Vert$的线性空间$V^n$就称为赋范空间，这里的$\Vert . \Vert$表示泛指的任何一种范数。

常用向量范数

$x$的1范数: $\Vert x \Vert_1 = \vert x_1\vert + \vert x_2\vert +\cdots +\vert x_n\vert$
$x$的2范数(欧式范数): {% math %}\Vert x \Vert_2 = (\vert x_1\vert^2 + \vert x_2\vert^2 +\cdots +\vert x_n\vert^2)^{\frac{1}{2}}{% endmath %}
$x$的$\infty$范数(最大范数): $\Vert x \Vert\_{\infty} = \max\_{1\leq i\leq n}\vert x\_i\vert$
$x$的$p$范数($p \geq 1$): {% math %}\Vert x \Vert_p = (\vert x_1\vert^p + \vert x_2\vert^p +\cdots +\vert x_n\vert^p)^{\frac{1}{p}}{% endmath %}

向量范数的几何意义

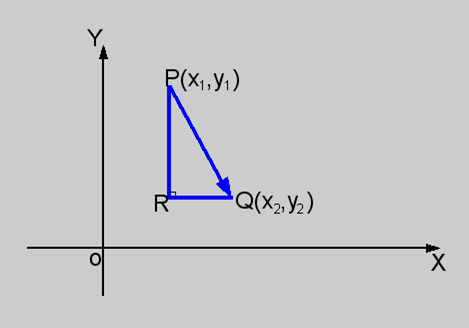
其实常用的几个范数在直观上是有几何意义的，如下所示:

$\Vert x\Vert_{\infty} = \max(\vert x_2-x_1\vert,\vert y_2-y_1\vert)$ 长的直角边
$\Vert x\Vert_1 = \vert x_2-x_1\vert + \vert y_2-y_1\vert$ 两直角边之和
{% math %}\Vert x\Vert_2 = \sqrt{(y_2-y_1)^2+(x_2-x_1)^2}{% endmath %} 斜边

向量范数

向量范数之间的关系

定义: 设$\Vert x\Vert_{\alpha}$与$\Vert x \Vert_{\beta}$是$n$维线性空间$V^n$上定义的任意两种范数，若存在两个与$x$无关的正常数$c_1,c_2$，使得:

$$ \begin{equation} c_1\Vert x\Vert_{\beta}\leq \Vert x \Vert_{\alpha}\leq c_2\Vert x \Vert_{\beta}, \forall x \in V^n \end{equation} $$

则称$\Vert x\Vert\_{\alpha}$与$\Vert x\Vert_{\beta}$是等价的

定理: 同一个有限维线性空间上不同的范数是等价的。

矩阵范数

定义

定义: 设$A$为$n\times n$的方阵矩阵，$\Vert \bullet \Vert$是以$A$为自变量的的实值函数，且满足条件:

非负性: $\Vert A \Vert\geq 0$,且$\Vert A \Vert=0$当前仅当$A=0$
齐次性: $\Vert\alpha A\Vert=\vert \alpha \vert \Vert A \Vert,\alpha\in R$
三角不等式: $\Vert A+B \Vert\leq \Vert A\Vert + \Vert B\Vert$
相容性: $\Vert AB \Vert\leq \Vert A\Vert\Vert B\Vert$

则称$\Vert A\Vert$为矩阵$A$的范数

常用矩阵范数

$\Vert A \Vert_1 = \max_{1\leq j\leq n}\sum\_{i=1}^n\vert a_{ij}\vert$ $A$的每列绝对值之和的最大值，称为{% math %}A{% endmath %}的列范数 .
$\Vert A \Vert_{\infty} = \max_{1\leq i\leq n}\sum_{j=1}^n\vert a_{ij}\vert$ $A$的每行绝对值之和的最大值，称为$A$的行范数 .
$\Vert A\Vert_{2}=\sqrt{\lambda_{max}(A^TA)}$ 称为$A$的2范数 ，其中$\lambda_{max}(A^TA)$为$A^TA$的特征值的绝对值的最大值
$\Vert A \Vert_{F}=\sqrt{\sum_{i=1}^{n}\sum_{j=1}^{n}\vert a_{i,j}\vert^2}$ 称为Frobenius范数 .

| $\Vert A \Vert_1$,$\Vert A \Vert_{\infty}$ | $\Vert A\Vert_{2}$ | $\Vert A \Vert_{F}$ | | 容易计算，使用最广泛 | 计算较复杂对矩阵元素比较敏感，性质较好，使用比较广泛 | 较少使用 |

谱半径

定义: 设$A\in R^{n\times n}$的特征值为$\lambda_1,\lambda_2,\cdots,\lambda_n$称

$$ \begin{equation} \rho(A) = \max\{\vert\lambda_1\vert,\vert\lambda_2\vert,\cdots,\vert\lambda_n\vert\} \end{equation} $$

为矩阵$A$的谱半径²

定理: 设$A$为$n$阶方阵，则对任意算子范数$\Vert \cdot \Vert$有

$$ \begin{equation} \rho(A) \leq \Vert A\Vert \end{equation} $$

证明:

根据算子范数的相容性,得到$\Vert Ax\Vert\leq\Vert A\Vert\cdot\Vert x\Vert$

将任意一个特征根$\lambda$所对应的特征向量$u$代入

$$ \begin{equation} \vert \lambda \vert\cdot\Vert u\Vert = \Vert \lambda u\Vert = \Vert Au \Vert \leq \Vert A \Vert\cdot\Vert u\Vert \end{equation} $$

即$\vert\lambda\vert\leq\Vert A\Vert$，所以$\rho(A) \leq \Vert A\Vert$

这个定理说明:矩阵A的谱半径不超过矩阵的任何一种算子范数

定理: 若$A$对称，则有$\Vert A\Vert_2=\rho(A)$

证明:

$\Vert A\Vert_{2}=\sqrt{\lambda_{max}(A^TA)}=\sqrt{\lambda_{max}(A^2)}$

又因为:若$\lambda$是$A$的一个特征根，则$\lambda^2$必是$A^2$的特征根.

所以，$A$中特征根绝对值最大的$\vert \lambda\vert_{max}$必满足:$\vert \lambda\vert_{max}^2 = \lambda_{max}(A^2)$

代入上式中，得到:

$$ \begin{equation} \Vert A\Vert_{2}=\sqrt{\lambda_{max}(A^TA)}=\sqrt{\lambda_{max}(A^2)}=\sqrt{\vert \lambda\vert_{max}^2}=\vert \lambda\vert_{max} \end{equation} $$

根据$\rho(A)$的定义，即得到$\Vert A\Vert_{2} = \rho(A)$

证明一个实值函数是一个范数，就是需要证明这个函数满足上述3个条件。 ↩
根据定义，显然有$\Vert A\Vert_{2}=\sqrt{\lambda_{max}(A^TA)}=\sqrt{\rho(A^TA)}$ ↩

Flyaway is the owner of this blog.

矩阵论学习笔记8-赋范线性空间与范数

向量范数

定义

常用向量范数

向量范数的几何意义

向量范数之间的关系

矩阵范数

定义

常用矩阵范数

谱半径

Reading Time

Published

Category

Tags

Contact