Logistic回归

在实际应用中，除了预测问题，其实更多的是 分类问题，回归问题和分类问题其实是非常相似的，主要区别是分类问题的输出变量Y是取有限个离散值的，而回归问题本质上是一个拟合问题，给定一组已知数据，选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据。

面对两个相似的问题，我们就要考虑能否用同样的算法来解决？之前学习过线性回归模型，其实只要对线性回归模型稍加修改，就能将其应用到 分类问题上面了，经过修改过的线性回归模型就被称为Logistic回归。具体修改方案如下:

假设对应的分类目标只有两类，即y∈0,1，回顾一下，在线性回归模型中，我们的预测函数为h_θ(x)，在分类问题中，我们将其稍加修改:

其实就是在原来的预测函数上叠加一个g(z)函数，而g(z)是如此定义的:

可以来看一下g(x)函数的图像:

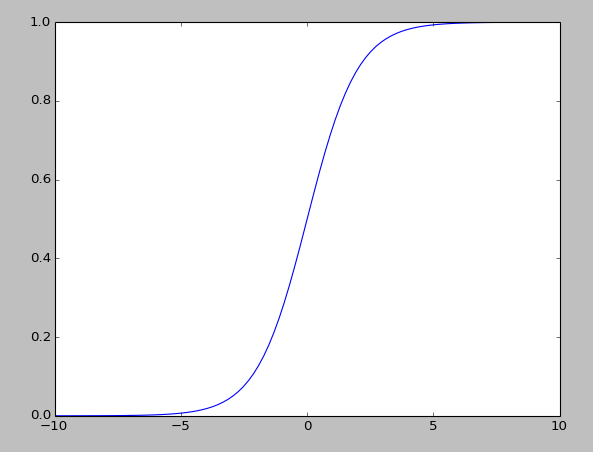
从图像中可以看出，函数值是永远固定在[0,1]之内的，其实这个g(z)函数就被称为Logistic函数或者sigmoid函数。因此，在这个Logistic函数的作用下，h_θ(x)就被固定在[0,1]之内，也即h_θ(x)∈[0,1]。

再次观察Logistic函数的图像，我们可以发现，x越大，其函数值越接近于1，x越小，其函数值越接近与0，因此我们用h_θ(x)来估计每个分类的概率值，即：

又因为我们的假设是一个二元分类问题，所以：

将上面两个等式合并:

接着，我们可以写出参数θ的似然函数:

这时，就可以依照在最小二乘法的概率解释中的推导过程一样，将这个关于θ的复杂似然函数转化为相对简单的对数函数:

现在的目标就是要使得这个似然函数最大化，可以回想一下我们在线性回归模型中所用的算法——梯度下降法，在此处我们也可以使用这个算法，使得θ=θ+α∇ℓ(θ)，需要注意的是，此处我们使用的加号而不是减号，因为我们要求的最大值而不是最小值。

对θ中的每一个分量进行求偏导(此时为了运算的方便，暂时当做只有一组数据)：

而又因为g(z)=11+e−z，所以

因此式子???可以进行如下的推导：

最终，我们得到了梯度上升法的递推公式:

到现在为止，我们已经得到了Logistic回归模型的学习算法了。

比较

这个公式???和线性回归模型 中的梯度下降法"长得"是一样的，但是其本质是完全不同的，在线性回归模型中，h_θ(x)是一个线性函数，而在Logistic回归中，h_θ(x)则不是一个线性函数，而是一个sigmoid函数。

在学习算法中，有三种学习模型是非常相似的，分别是线性回归模型 、Logistic回归和感知机模型 ，它们不管在模型的建立还是在算法的求解上都非常的相似¹，但是它们之间也存在着不同的地方。

首先是线性回归模型 ，它主要使用来对一系列的点进行拟合的，它的输出值(h_θ(x))是任意的预测值。

而感知机模型则是一种典型的简单分类器，它的输出值(h_θ(x))只能是固定的有限的几个类别，在二元分类问题中，其输出值(h_θ(x))只能0或1，即h_θ(x)∈{0,1} filename 最后是本文的主角，Logistic回归，某种程度上，我觉得它是介于上面两种模型之间的"中间模型"，它的输出值(h_θ(x))虽然也是固定在有限的范围内，但是却是连续的，而不像感知机那样，全是离散的值，在二元分类中，其输出值是h_θ(x)∈[0,1]。

参考资料

• 斯坦福公开课《机器学习》第三集及其配套讲义
• logistic回归的一些直观理解

Share on: Twitter ❄ Facebook ❄ Email

---

---