在很多应用场景中，我们都是需要一种动态的数据存储结构，用来存储数据，并且这样的数据结构能够采用字典的方式来访问，也即可以通过关键字访问其中的元素.而散列表(Hash)就是用来实现这样的字典操作的常用方式。一个字典结构，至少需要具有如下三个操作:
INSERT: 插入SEARCH: 查找DELETE: 删除
最理想的情况下，上述三种操作都应该在常数时间内完成。
直接寻址表
直接寻址表是最简单的一种的字典操作的实现方式，其实从我的理解上来看，它本质上就是一个数组，只不过字典的关键字恰好就是整型的数字，把关键字直接作为下标来使用。具体的过程可以用下图来表示:
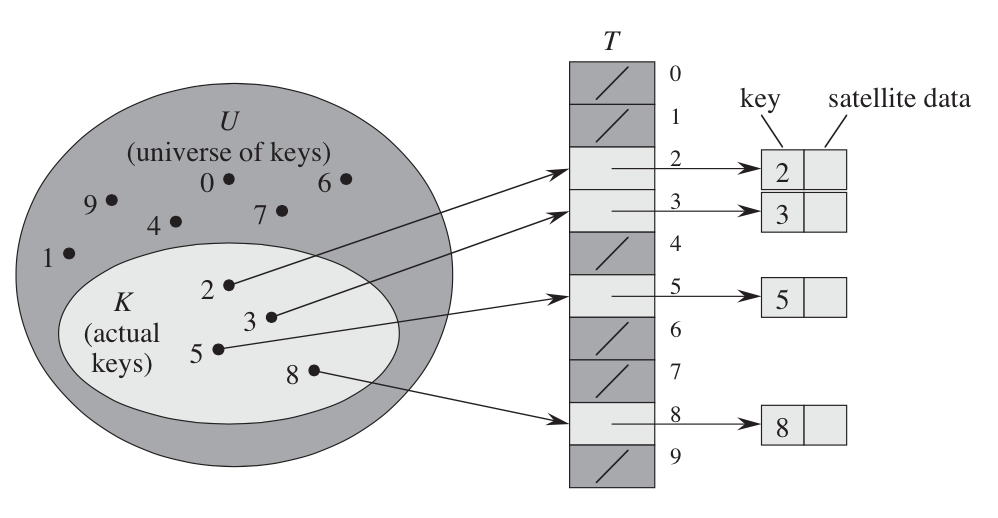
其中，\(U\)是关键字的全域，\(T\)是一个数组，数组中存储的元素是一个指针，指向了卫星数据.这种实现方式非常的简单，而且插入,查找,删除这三种操作都是\(O(1)\)的。
然而，从图中就可以看到，这样的实现方式有一个最大的问题，那就是会导致大量的空间被浪费 :如果关键字的全域非常大，但真正被使用的关键字又非常少，而同时\(T\)的大小又是由\(\vert U \vert\)决定的，因此大量的空间没有被使用，造成了浪费。
散列表
散列表的基本思想就是使得\(T\)的大小要远小于关键字全域\(U\)，也即需要满足\(\vert T\vert \ll \vert U \vert\). 具体做法就是利用一个称为散列函数的函数\(h\)，将关键字1\(k\)从全域\(U\)映射到散列表中，用符号来表示就是:
其中，全域\(U\)的大小为\(n\)，而散列表\(T\)的大小为\(m\)，且\(m \ll n\).
如此的做法就可以极大的减少了需要存储的空间，从原来的\(n\)降低到了\(m\)，这个过程可以用下图来说明:
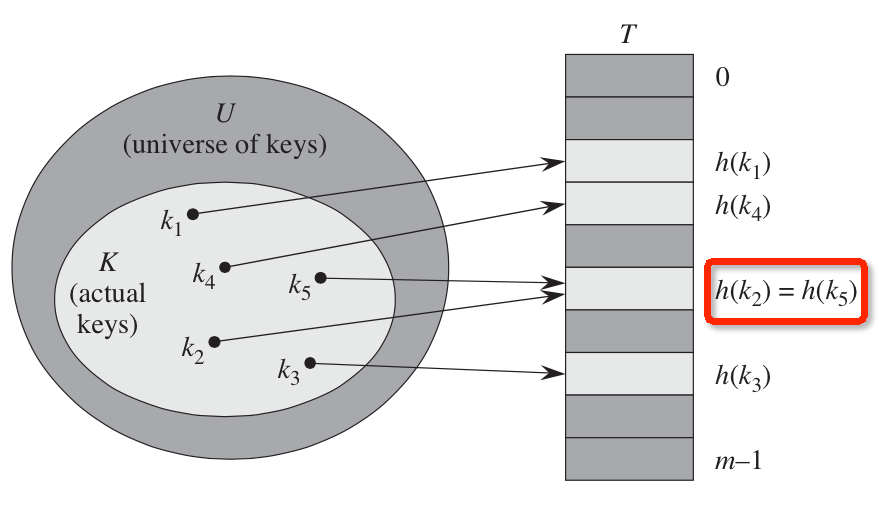
但是，如此的做法会导致另外一个问题: 两个不同的关键字会被映射到同一个位置上(如上图中红色圈出来的部分。)这种情况被称为是冲突。
根据鸽巢原理，这样的冲突是不可避免，必然会发生的。因此，对于这种情况，我们需要设计一种策略来处理这种发生冲突的情况。
处理冲突的情况一般有两个方面:
总结
根据上面的说明，其实我们就可以确定散列表的两大要素:
- 一个好的散列函数
- 一个冲突的解决方案
常见的散列函数有除法散列、乘法散列和全域散列，常用的冲突解决方案是链接法和开放寻趾法。
具体的散列函数和冲突解决方案会在后续的笔记中的陆续说明。
-
需要注意的是，这里的关键字可以是任意类型的，不一定是整型的。 ↩