第一章
这一章主要介绍了算法的基本概念以及其应用范围,对于算法的定义,原文摘录如下:
算法: 算法是任何良定义的计算过程,该过程取某个值或值的集合作为输入并产生某个值或值的集合作为输出.
需要理解是的,不是世界上所有的问题都是有有效算法的,有一些问题我们无法求得其精确解,只能求得其近似解。
第二章
本章一开始就抛出了一个排序问题,给出了插入排序的算法,这是最基本的一个排序算法。本书的算法描述都是用为伪代码给出的,通俗易懂。
然后以排序算法为例,说明算法分析的框架,主要是使用了RAM计算模型,算法复杂度可以用算法的运行时间来衡量,可以将其看成是一个以算法输入规模为参数的函数。
第三部分介绍归并排序的算法,并且分析了其运行效率,这里引出算法设计的一个策略:分治策略.
简单来说,分为分支策略分为三步:
- 分解(Divide)
- 解决(Conquer)
- 合并(Combine)
后面应该还会有相应的章节介绍分治策略,这里就只是简单说明一下。
第三章
本章主要说明了算法的渐进表示法,具体有几个渐进记号需要掌握:
Θ记号
对一个给定的函数g(n),用Θ(g(n))来表示以下函数的集合:
Θ(g(n))={f(n):存在正常量c1,c2和n0,使得对所有n≥n0,有0≤c1g(n)≤f(n)≤c2g(n)}
从定义中可以看到,其实f(n)是被g(n)"夹住"了,通常称g(n)为f(n)的一个渐进紧确界.
O记号
对一个给定的函数g(n),用O(g(n))来表示以下函数的集合:
O(g(n))={f(n):存在正常量c和n0,使得对所有n≥n0,有0≤f(n)≤cg(n)}
我们通常使用O记号来给出函数在一个常量因子内的上界,它称为渐进上界.一般来说,O可以用来一个算法的最坏情况,因为它限制了函数的上界。
Ω记号
与O相对的,Ω给出了函数的渐进下界.对于给定的函数g(n),用Ω来表示以下函数的集合:
Ω(g(n))={f(n):存在正常量c和n0,使得对所有n≥n0,有0≤cg(n)≤f(n)}
上述三种记号是在算法分析中经常会被使用到的,关于这三种记号,还有有一个定理:
定理: 对任意两个函数f(n)和g(n),我们有f(n)=Θ(g(n)),当且仅当f(n)=O(g(n))且f(n)=Ω(g(n))
其他的记号
除了上述三种记号以外,还有两种不太用到的记号,分别是o和ω,其定义分别如下:
o(g(n))={f(n):对任意正常量c>0,存在常量n0>0,使得对所有n≥n0,有0≤f(n)<cg(n)}
O和o的定义很类似,主要区别是在f(n)=O(g(n))中,界0≤f(n)≤cg(n)对某个常量c>0成立,但在f(n)=o(g(n))中,界0≤f(n)<cg(n)对所有常量c>0成立。
ω(g(n))={f(n):对任意正常量c>0,存在常量n0>0,使得对所有n≥n0,有0≤cg(n)<f(n)}
关于Θ,O,Ω这三种记号的理解,可以用下图来直观的表示:
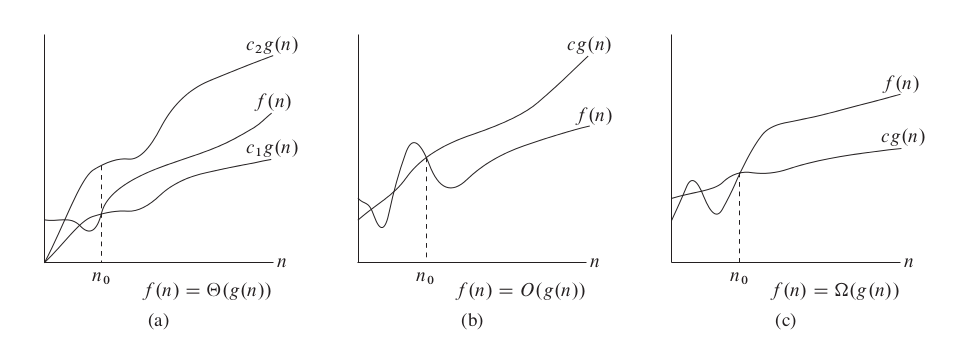
最后需要说明的一点是,上述的这五种记号都表示的是函数的集合,而不是具体的某一个函数,因此f(n)=O(n2)其实表示的是f(n)∈O(n2)),只是为了方便所以才写成等号的。