写在前面
这个算法的分析其实上周就想写了,可惜一直忙于上课和作业,没有时间仔细考虑这个问题。只是依稀记得以前上课的时候做过一个递归的求全排列的算法,但是对于长度为n的串的全排列的可能情况是n!,这个增长太快了,使用递归的话几乎不太可能满足日常的需求,从这个角度来说,全排列的递归算法只能作为学习递归算法的一个例子吧。本文将从递归算法开始,分析几个目前常用的生成全排列算法,包括字典序算法、Johnson-Trotter算法和多进制算法。
递归算法
对于求一个序列的全排列,最直接的想法肯定就是采用递归的方法了,因为根据阶乘的定义n!=n\*(n−1)!,因此递归的过程就是:
- 递归式:在每一次的递归层次中求出(n−1)个元素的全排列。
- 递归边界条件:当元素个数为1的时候,直接返回该元素。
但是在具体的实现过程中,如何处理返回的n−1个元素的全排列又有很多不同的方法,这里主要介绍两种。
插入法
这种方法有点类似于插入排序,当通过递归过程返回n−1个数的全排列的时候,我将第n个数插入到这些排列的空隙中,形成新的排列。举例来说,对于a={0,1,2,3}来说,首先取出第一个元素0,然后通过递归生成{1,2,3}的全排列:
#!python
{
{1,2,3},
{1,3,2},
{2,1,3},
{2,3,1},
{3,1,2},
{3,2,1},
}
然后对于生成的每一个排列,将0在每一个可能的位置插入:
#!python
{
{0,1,2,3},
{1,0,3,2},
{1,2,0,3},
{1,2,3,0}, #完成了对{1,2,3}的插入
{0,1,3,2},
{1,0,3,2},
{1,3,0,2},
{1,3,2,0}, #完成了对{1,3,2}的插入
...
}
按照这样的顺序,我们就能够依次生成原序列的所有排列情况了。可以看到,按照这样的算法, 每一次首元素都会被插入到不同的位置中,这一点是和下面要介绍的另外一种递归方法的本质区别。
下面给出插入法递归的代码:
代码1:
#!python
def perm(arg):
if len(arg)==0:
return [[]]
else:
#得到n-1的排列
t = perm(arg[1:])
order = []
#遍历每一个排列
for item in t:
#在每一个排列的可能位置中插入当前元素
for (index,x) in enumerate(item):
tmp = item[:]
tmp.insert(index,arg[0])
order.append(tmp)
tmp = item[:]
tmp.append(arg[0])
order.append(tmp)
return order
固定首元素
在这种方法中,我们不需要每次都要将首元素插入到不同位置中,在递归过程中,我们会尝试所有可能的首元素,生成不同元素作为首元素时排列,举例来说,对于a={0,1,2,3},我们首先选取0作为首元素,然后固定住0,向下递归生成{1,2,3}的排列,然后,直接将0和生成的排列拼接起来(而不是插入),如下所示:
下面是{1,2,3}的全排列
:::python
{
{1,2,3},
{1,3,2},
{2,1,3},
{2,3,1},
{3,1,2},
{3,2,1},
}
直接将这些排列和0拼接,形成:
:::python
{
{0,1,2,3},
{0,1,3,2},
{0,2,1,3},
{0,2,3,1},
{0,3,1,2},
{0,3,2,1},
}
完成拼接之后,选取1作为首元素,向下递归生成{0,2,3}的全排列,然后,将1和生成的排列拼接起来;之后选取2作为首元素,重复上述过程,直到所有元素都作为首元素固定过。
下面给出代码:
代码2: #!python def perm(arg,order,k=0): if k >= len(arg): order.append(arg[:]) return else: for i in range(k,len(arg)): #交换首元素 arg[i],arg[k] = arg[k],arg[i] #递归调用 perm(arg,order,k+1) #换回原来的位置 arg[i],arg[k] = arg[k],arg[i]
上面的代码是我自己写的,但是另外我在V2EX上还看到过同样算法的更加简洁的代码:
代码3:
#!python
def all_perm(l):
if not l:
return [[]]
return [[a] + b for a in l for b in all_perm(_remove(l, a))]
def _remove(l, item):
tmp = l[:]
tmp.remove(item)
return tmp
字典序法
除了递归的方法,其实还有很多其他非递归的方法可以用来计算一个序列的全排列。其中有一个算法被称为字典序算法,据说STL中的Next_permutation也是用这个字典序算法实现的1。这个算法的核心思想就是,对于每一种可能排列的情况,我们都想办法使其与某种顺序建立对应关系,这种关系式一一对应的,这样我们就能通过遍历得到的某种顺序来生成全排列,这样就能避免递归过程了。这种按照某种顺序来生成全排列的方法就被称为是字典序。
很显然,最重要的是如何才能找到这样一种一一对应的顺序关系,此处继续用a={0,1,2,3}来说明字典序算法的过程。
要找到一种顺序关系,我们就首先要定义大小关系,对于两个序列{0,2,1,3}和{0,2,3,1}来说,序列{0,2,3,1}要比{0,2,1,3}大,比较的方法是从前到后依次比较相同位置上的元素,如果相同则继续比较下一个元素,直到遇到一个不同的元素,元素值大的序列就大于元素值小的序列。按照这样的大小关系形成的序列的顺序,就是字典序。可以看到,最小的序列一定是{0,1,2,3},最大的序列是{3,2,1,0}。而字典序算法就是从字典序中最小的序列开始,一直不停寻找下一个仅比上一个序列大的序列,直到到达最大的序列。2
现在的问题就变成了,如何从当前状态生成一下个状态?
字典序算法是这样做的(假设当前排列是a[1⋯n]):
-
从a中找到满足a[k]<a[k+1]的k的最大值,即k=max{i‖a[i]<a[i+1]}(0≤i<n−1),如果不存在这样的k,那就是说已经达到字典序最大的序列了3。
-
从a[k+1⋯n]中寻找比a[k]大的数中的最小数a[j],即j=min{i‖a[i]>a[k]}(k<i≤n−1)
-
交换a[k]和a[j],并将a[k+1⋯n]中的元素全部倒序。
经过上述三步,得到的序列就是a[1⋯n]在字典序中的下一个序列了。
我想看到这里,很多人都是一头雾水了吧,这三步只是告诉你How-to-do而不是Why-to-do,这里简略给出一个说明4:
首先应该知道,根据字典序的定义,越是小的数排在前面,则整个序列越小。
- 第一步中找到的a[k],其实它是有这样的性质的:在k右侧的所有元素都是从大到小排列的
- 第二步中找到的a[j]是用来和a[k]交换的,根据a[j]满足的条件,可以得出这样的结论:在a[k+1⋯n]中,a[k]是仅次于a[j]的数。而将他们交换之后,能保证整个序列是最小增长的。
- 但是由于a[k+1⋯n]中是从大到小排列的,因此需要将这部分倒序,来使得序列进一步减小,使其成为仅大于原始序列的序列。
代码4:
#!python
def nextstate(arg):
flag = False
#步骤1
for i in range(len(arg)-2,-1,-1):
if(arg[i] < arg[i+1]):
flag = True
break
if flag:
k = i
else:
return False
#步骤2
for i in range(len(arg)-1,k,-1):
if arg[i] > arg[k]:
break
j = i
#步骤3
arg[j],arg[k] = arg[k],arg[j]
t = arg[k+1:]
t.reverse()
arg[k+1:] = t
return True
def dictgenerate(arg):
myarg = list(range(len(arg)))
order = []
t = []
for i in myarg:
t.append(arg[i])
order.append(t)
while True:
t = []
flag = nextstate(myarg)
if flag == False:
break
for i in myarg:
t.append(arg[i])
order.append(t)
return order
关于代码
如果有读者运行我上述的代码,大概会发现其实递归的算法和字典序的算法效率上相差不大,甚至有时候递归比字典序还快。但是,我想说的是,出现这样的现象不是 算法的问题,而是Python语言的问题,Python在很多方面都有着非常不错的特点的,但是在运行效率上却不是很高(相对来说它的开发效率很高),因此会出现递归和字典序效率差不多的现象。从这个角度来说,Python其实并不是一门适合学习算法时所使用的语言,它更多的偏向于解决实际的问题,而不是编程细节。
如果用C++重新实现上述的算法,你就会发现其实递归要比字典序算法慢得多。
参考资料
补充
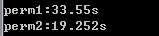
后来越想越不好,明明应该是在讲算法的,但是运行结果却不能证明算法的高效,干脆直接装了个C++编译器,将上述两个递归和非递归的算法重新实现了一遍:
递归算法:
#!cpp
void perm2(int *arg,int n,int k)
{
int i;
if(k>=n)
{
//print
}
else
{
for(i = k;i < n;++i)
{
swap(arg[i],arg[k]);
perm1(arg,n,k+1);
swap(arg[i],arg[k]);
}
}
}
字典序算法:
#!cpp
bool nextstate(int *arg,int n)
{
int i;
bool flag=false;
int k,j;
int start,end;
//step 1
for(i = n-2;i >= 0;--i)
{
if(arg[i] < arg[i+1])
{
k = i;
flag = true;
break;
}
}
if(flag==false)
{
return false;
}
//step2
for(i = n-1 ; i > k ; --i)
{
if(arg[i] > arg[k])
{
j = i;
break;
}
}
//step3
swap(arg[k],arg[j]);
for(start = k+1,end=n-1 ; start<end ; ++start,--end)
{
swap(arg[start],arg[end]);
}
return true;
}
void perm3(int *arg,int n)
{
int myarg[n];
int i;
for(i = 0;i < n; ++i)
{
myarg[i] = i;
}
//print
while(true)
{
if(nextstate(myarg,n))
{
//print
}
else
{break;}
}
}
下图是运行的结果(12个元素的全排列):