引言
任何一个学习计算的人都应该了解什么是NP和NP-Complete问题,之前虽然学过,但是很长一段时间没有回顾,基本就已经忘的差不多了。 最近算法课讲到这个问题,本着「好好学习,天天向上」的态度,重新复习一下这几个基本概念。
如果只是需要快速知道什么是NP和NP-Complete,请直接跳跃到最后总结部分。
「问题」的定义
我们都知道NP和NP-Complete其实是对不同类别问题的描述,有些是「可解」的问题,而有些是「不可解」的问题。 但是,在区分什么是「可解」和「不可解」之前,我们更需要理解,什么是「问题」.
一个抽象问题Q是一个定义在问题实例集合I和问题解集合S上的一个二元关系。 比如,在最短路径问题中,问题实例就是一个图和两个点组成的三元组,而其对应的解就是一个顶点的序列。
抽象问题通常分为两个类别:
- 优化问题: 通常需要求得某个值的最大值或最小值
- 判定问题: 解为0或1的问题
NP理论关注的只是其中的判定问题。 然而实际上,优化问题和判定问题是可以相互转化的。 比如求最短路径问题,很明显这是一个优化问题,但是我们可以将问题改写成一个判定问题.
- 最短路径的优化问题版: 给定一个图G及其上的两个顶点s,v,请找出s到v的最短路径。
- 最短路径的判定问题版: 给定一个图G,及其上的两个顶点s,v和一个常数k,请判定图G是否存在一条从s到v且长度最多为k路径。
编码
我们都知道,计算机底层都是二进制的代码。 因此,为了使得计算机程序能够求解一个抽象问题,我们需要对抽象问题进行编码操作。 我们通常都是采用二进制来对抽象对象进行编码的。 抽象对象集合S的编码是从S到二进制串集合的一个映射e。 举例来说,数字17的编码就是e(17)=10001.
其实从抽象概念和编码概念上来说,我们所使用的语言也是一种编码,而我们脑海中的东西才是真正的抽象概念。
我们将一个以二进制序列为集合的实例集合称为具体问题(Concrete Problem)1.
P和NP
在上述的铺垫之后,我们现在可以定义什么才是真正的P了。
- P: 在多项式时间可解决的具体判定问题的集合。
- NP: 在多项式时间可验证的具体判定问题的集合。
可验证是指,在给定一个问题及其可能的一个解,我们能否判断这个解是否是当前问题的解。 从直觉上来说可验证要比可解决要容易得多,因此,我们可以认为P⊆NP. 问题的关键在于,P是不是NP的一个真子集,这个问题困扰了CS理论界很多年了,但依然没有定论。 不过大多数人都认为P≠NP.
规约
此处的规约是指,存在一个多项式时间的算法f能够将问题A转化为问题B,也即f能够将任意一个实例I∈A转化为f(I)∈B,同时存在另外一个多项式时间的算法h,将问题B的解转化为问题A的解,也即能够将f(I)的解S转化为I的解h(S). 下图比较直观的说明这个过程。
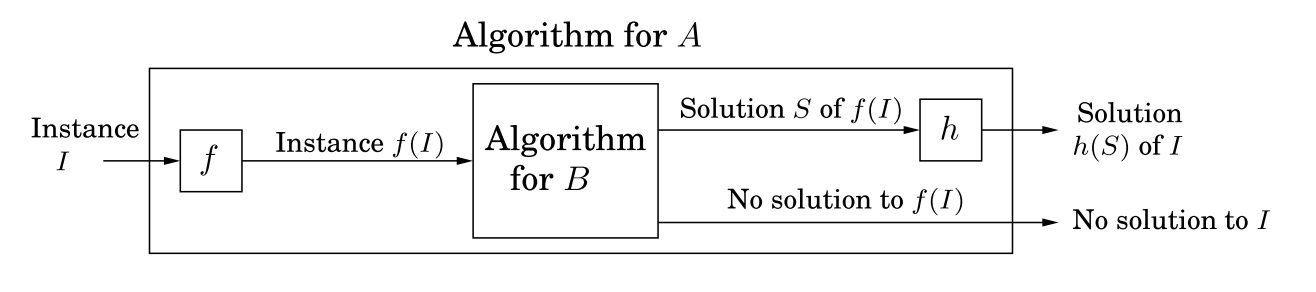
规约在NP理论中是一个非常有用的工具,我们通常用A⟶B表示A能够规约为B. 有时候也可以表示成A≤pB. 这形象地说明了问题A的难度是「小于等于」问题B的.
根据定义,我们知道,如果我们能够找到一个算法高效的解决问题B,那么我们一定也能找到一个算法高效的解决A. 但是,倒过来却并不成立,如果我们一个算法能高效解决A,并不代表我们能找到一个算法高效的解决B.
在A⟶B中,问题的能难度随着箭头的方向而增加。 其实,规约最大的作用在于证明如果我们能知道解决A是非常困难的,那么解决B至少是同样困难的。 也就是说,面对一个新问题X,如果我们能将某个已知的非常困难的问题A规约到X,那么我们就能证明X至少是同样苦难的,因此不需要花费大量的时间去设计一个求取精确解的算法,我们可以转而寻找可行解。
至于如何规约,这已经超出我的需求,我觉得作为一个非专业研究NP问题的人来说,我并不需要知道如何进行规约(有些规约很简单,有些却很复杂)。 我只需要知道基本概念及其之间的关系,这已经满足的应用需求了。
NP-Complete
利用规约,我们能够给出NP-Complete的定义:
NP-Complete: 如果所有的NP问题都能规约到一个问题,那么这个问题就是NP-Complete.
另外还有一种来源于「算法导论」的定义方式:
一个问题Q是NP-Complete,当它同时满足如下的条件: 1. Q∈NP 2. 对于每一个Q′∈NP满足Q′≤pQ
很显然,这两个定义其实表达的是同一件事。
根据这个定义,我们可以知道:
- NP-Complete既可以看成是一个问题,也可以看成是一个问题集合。 因为属于NP-Complete的问题必然是可以相互规约的,也即可以看成是同一个问题。
- NP-Complete是NP中最难的那一部分问题。
另外,在Introductino to Algorithm的定义中,如果某个问题Q只满足第二个条件,但不满足第一个条件,那么这个问题是NP-Hard的。 可以认为,NP-Hard是比NP-Complete还要难的问题的。
NP-Complete问题到目前为止还没人能找出其多项式时间内的解,如果我们在未来的某一天中能够找到一个NP-Complete问题多项式时间内的解,那么我们就能证明其实P=NP. 因为NP-Complete代表的是NP中最难的那部分问题,如果这部分问题能在多项式时间内解决,那么整个NP就都能在多项式时间内解决,也即NP=P.
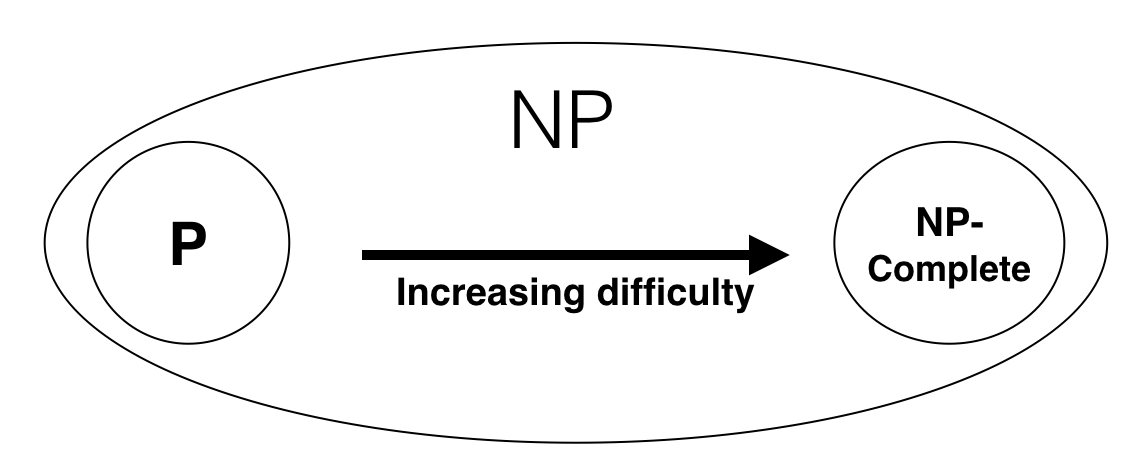
下图比较清晰的说明了P、NP和NP-Complete的关系.
下表列举了一些NP-Complete和P问题
| Hard Problems(NP-complete) | Easy Problems(P) |
|---|---|
| 3SAT | 2SAT, Horn SAT |
| Longest Path | Minimum Spanning Tree |
| 3D Matching | Bipartite Matching |
| Knapsack | Unary Knapsack |
| Independent Set | Independent Set on Trees |
| Integer Linear Programming | Linear Programming |
| Rudrata Path | Euler Path |
| Balanced Cut | Minimum Cut |
总结
- P: 能够在多项式内解决的问题集合
- NP: 不一定能够在多项式内解决,但是给定答案,能够在多项式时间内验证答案的问题集合
- NP-Complete: NP中的最难的那一部分问题。
- NP-Hard: 比NP-Complete还要难的问题。
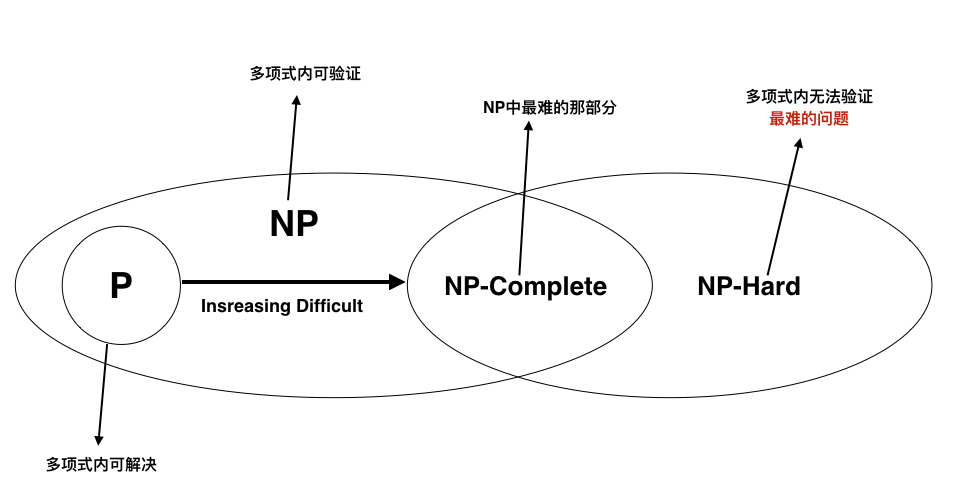
一图胜千言,这几个概念可以用一张图来说明:
参考资料
- Algorithms (Dasgupta, Papadimitriou, Vazirani)
- Introduction to Algorithms (Cormen, Leiserson, Rivest, Stein)
更新日志
- 2016-10-8 完成初稿并发布。
- 2016-10-10 增加规约的≤p符号、算法导论的关于NP-Complete和NP-Hard的定义、画出NP问题的总概念图。
- 2016-10-11 修正几处输入错误。
- 2016-10-12 增加NP-Complete和P的问题举例列表。
-
有一本书就叫「具体数学」 ↩