商人过河问题常常出现在一些电视剧中作为考察智力的题目,其实这类问题是有迹可循的,本文将从数学建模和算法的角度来分析这一问题,给出具体的解法。
问题描述
三名商人各带一个随从乘船渡河。现此岸有一小船只能容纳两人,由他们自己划行。若在河的任一岸随从人数比商人多,他们就可能抢劫财物。不过如何乘船渡河的大权由商人们掌握。商人们怎样才能安全过河呢?
分析
大多数人看到这类问题的第一反应就是一个方案一个方案去试,直到找到一个符合条件的方案。但是这样的寻找过程就像是没头苍蝇一样,没有章法可循。我们首先可以对原题进行建模,将原来用文字描述的问题转化为数学的语言,再从数学角度对其进行搜索。
建模
首先假设商人和仆人都在北岸,他们的目的地是南岸。那么我们可以用(x,y)表示在北岸的商人(x)和仆人(y)的人数((x,y)∈{0,1,2,3}),用Sk=(xk,yk)表示第k次渡河前北岸的商人和仆人的人数,称其为一个状态。用dk=(uk,vk)表示第k次渡河时,船上的商人和仆人的人数({(uk,vk)‖0<uk+vk<=2})。将dk称为一次转移。因为k为奇数时,是从北岸到南岸,而k为偶数时是从南岸到北岸,所以Sk随dk的变化规律是:
对于状态Sk和转移dk来说,它必须满足以下三个条件,才能被称为是允许转移集合:
- xk>=yk
- xk+(−1)kuk>=yk+(−1)kvk
- 3−xk+(−1)kuk>=3−yk+(−1)kvk
第一个条件是保证渡河前北岸商人数不小于仆人数,第二个条件是保证渡河后北岸的商人数不小于仆人数,第三个条件是保证渡河后,南岸的商人数不小于仆人数。
因此,原问题就转化为,寻找一个转移序列{dk‖k=1,2...n},使得Sk由初始状态S1=(3,3)经有限步n到达状态Sn=(0,0),并且中间的每一次转移都属于允许转移集合。1
求解
那么,我们应该如何来寻找这样一个转移序列dk呢?这其实是一个多步决策问题,但也可以把它看成一个图的问题。在直角坐标系中,将每一个状态Sk对应于图中的每一个点,如图所示:
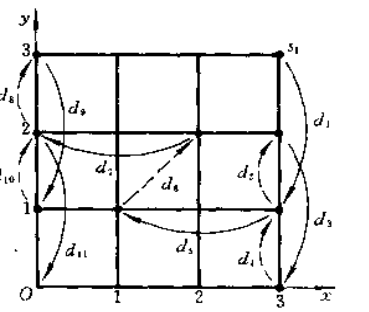
dk表示沿着方格移动1格或2格,当k为奇数时,向左,下方移动,k为偶数时,向右、上方移动。这样,我们的任务就变成了寻找从S1=(3,3)到原点(0,0)的一条路径,且这条路径上的每一次转移都属于允许转移集合。
算法
有了上述的思路以后,求解该问题就变得简单了,只要利用图论算法中的最简单的广度或深度遍历就行了2,唯一的不同是,在遍历每一个点的时候,都需要判断一下此次转移是否满足上述的三个条件。
最后贴出代码:
#!python
#coding:utf-8
"""
Author: Flyaway - flyaway1217@gmail.com
Date: 2013-08-12 13:57:31
Last modified: 2013-08-12 14:52:47
Python release: 3.3.2
"""
def issafe(state,d):
if state[1] > state[0] and state[0] != 0:
return False
elif state[1] + d[1] > state[0] + d[0] and state[0] + d[0] !=0:
return False
elif 3 - (state[1] + d[1]) > 3 - (state[0] + d[0]) and 3 - (state[0] + d[0]) != 0 :
return False
else:
return True
def explore(state,num,order,lastmove=(0,0)):
#设置递归层数限制,否则会进入无限递归
if num >= 20:
return False
if state == (0,0):
order.append(state)
return True
#运输规则
d = [(0,1),(0,2),(1,0),(1,1),(2,0)]
for item in d:
if item == lastmove:
continue
realitem = (item[0] * ((-1)**num) , item[1] * ((-1)**num))
if issafe(state,realitem) == True:
nextstate = ( (state[0] + realitem[0]) , ( state[1] + realitem[1]) )
if explore(nextstate,num+1,order,item) == True:
order.append(state)
return True
def main():
state = (3,3)
order = []
explore(state,1,order)
print(order)
if __name__ == '__main__':
main()
参考资料
- 《数学建模》姜启源